Set and multiset containers sort their elements automatically according to a
certain sorting criterion. The difference between the two is that multisets
allow duplicates, whereas sets do not.
Figure: Sets and Multisets
To use a set or multiset, you must include the header file <set>:
There, the type is defined as a template class inside namespace std:
The elements of a set or multiset may have any type T
that is assignable, copyable, and comparable according to the sorting criterion.
The optional second template argument defines the sorting criterion. If a
special sorting criterion is not passed, the default criterion less is used. The function object less sorts the elements by comparing them with operator <. The optional third template parameter
defines the memory model. The default memory model is the model allocator, which is provided by the C++ standard
library.
The sorting criterion must define "strict weak ordering." Strict weak
ordering is defined by the following three properties:
-
It has to be antisymmetric.This means for operator <: If x < y is true, then y < x is false.This means for a predicate op(): If op(x,y) is true, then op(y,x) is false.
-
It has to be transitive.This means for operator <: If x < y is true and y < z is true, then x < z is true.This means for a predicate op(): If op(x,y) is true and op (y,z) is true, then op(x,z) is true.
-
It has to be irreflexive.This means for operator <:x < x is always false.This means for a predicate op(): op(x,x) is always false.
Abilities of Sets and Multisets
Like all standardized associative container classes, sets and multisets are
usually implemented as balanced binary trees. The standard does not specify
this, but it follows from the complexity of set and multiset operations.
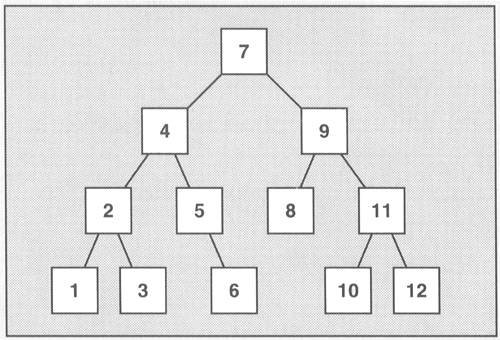
Figure: Internal Structure of Sets and Multisets
The major advantage of automatic sorting is that a binary tree performs well
when elements with a certain value are searched. In fact, search functions have
logarithmic complexity. For example, to search for an element in a set or
multiset of 1,000 elements, a tree search (which is performed by the member
function) needs, on average, one fiftieth of the comparisons of a linear search
(which is performed by the algorithm).
However, automatic sorting also imposes an important constraint on sets and
multisets: You may not change the value of an element directly because
this might compromise the correct order. Therefore, to modify the value of an
element, you must remove the element that has the old value and insert a new
element that has the new value. The interface reflects this behavior:
-
Sets and multisets don't provide operations for direct element access.
-
Indirect access via iterators has the constraint that, from the iterator's point of view, the element value is constant.
Set and Multiset Operations
Create, Copy, and Destroy Operations
Table: lists the constructors
and destructors of sets and multisets.
| Operation | Effect |
| set c | Creates an empty set/multiset without any elements |
| set c(op) | Creates an empty set/multiset that uses op as the sorting criterion |
| set c1(c2) | Creates a copy of another set/multiset of the same type (all elements are copied) |
| set c(beg,end) | Creates a set/multiset initialized by the elements of the range [beg,end) |
| set c(beg,end, op) | Creates a set/multiset with the sorting criterion op initialized by the elements of the range [beg,end) |
| c.~set() | Destroys all elements and frees the memory |
Here, set may be one of the following:
| set | Effect |
| set<Elem> | A set that sorts with less<> (operator <) |
| set<Elem,0p> | A set that sorts with 0p |
| multiset<Elem> | A multiset that sorts with less<> (operator <) |
| multiset<Elem,0p> | A multiset that sorts with 0p |
You can define the sorting criterion in two ways:
Note that the sorting criterion is also used to check for equality of the elements. Thus, when the default sorting criterion is used, the check for equality of two elements looks like this:
<
-
As a template parameter.
For example:
In this case, the sorting criterion is part of the type. Thus, the type system ensures that only containers with the same sorting criterion can be combined. This is the usual way to specify the sorting criterion. To be more precise, the second parameter is the type of the sorting criterion. The concrete sorting criterion is the function object that gets created with the container. To do this, the constructor of the container calls the default constructor of the type of the sorting criterion. See page 294 for an example that uses a user-defined sorting criterion.
-
As a constructor parameter.
In this case, you might have a type for several sorting criteria, and the initial value or state of the sorting criteria might differ. This is useful when processing the sorting criterion at runtime and when sorting criteria are needed that are different but of the same data type. See page 191 for a complete example.
Note that the sorting criterion is also used to check for equality of the elements. Thus, when the default sorting criterion is used, the check for equality of two elements looks like this:
<
This has three advantages:
-
You need to pass only one argument as the sorting criterion.
-
You don't have to provide operator == for the element type.
-
You can have contrary definitions for equality (it doesn't matter if operator == behaves differently than in the expression). However, this might be a source of confusion.
However, checking for equality in this way takes a bit more time. This is
because two comparisons might be necessary to evaluate the previous expression.
Note that if the result of the first comparison yields true, the second comparison is not evaluated.
By now the type name of the container might be a bit complicated and boring,
so it is probably a good idea to use a type definition. This definition could be
used as a shortcut wherever the container type is needed (this also applies to
iterator definitions):
The constructor for the beginning and the end of a range could be used to
initialize the container with elements from containers that have other types,
from arrays, or from the standard input.
Nonmodifying Operations
Sets and multisets provide the usual nonmodifying operations to query the size and to make comparisons (Table below).
| Operation | Effect |
| c.size() | Returns the actual number of elements |
| c.empty () | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2) ) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1) ) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to !(c1<c2)) |
Comparisons are provided only for containers of the same type. Thus, the elements and the sorting criterion must have the same types; otherwise, a type error occurs at compile time. For example:
The check whether a container is less than another container is done by a
lexicographical comparison. To compare containers of different
types (different sorting criteria).
Special Search Operations
Sets and multisets are optimized for fast searching of elements, so they
provide special search functions. These functions are special versions of general algorithms that have
the same name. You should always prefer the optimized versions for sets and
multisets to achieve logarithmic complexity instead of the linear complexity of
the general algorithms. For example, a search of a collection of 1,000 elements
requires on average only 10 comparisons instead of 500.
| Operation | Effect |
| count (elem) | Returns the number of elements with value elem |
| find(elem) | Returns the position of the first element with value elem or end() |
| lower _bound( elem) | Returns the first position, where elem would get inserted (the first element >= elem) |
| upper _bound (elem) | Returns the last position, where elem would get inserted (the first element > elem) |
| equal_range (elem) | Returns the first and last position, where elem would get inserted (the range of elements == elem) |
The find() member function searches the first element that has the value that was passed as the argument and returns its iterator position. If no such element is found, find() returns end() of the container.
lower_bound() and upper_bound() return the first and last position
respectively, at which an element with the passed value would be inserted. In
other words, lower_bound() returns the position of the
first element that has the same or a greater value than the argument, whereas
upper_bound() returns the position of the first element
with a greater value. equal_range() returns both return
values of lower_bound() and upper_bound() as a pair. Thus, it returns the range of
elements that have the same value as the argument. If lower_bound() or the first value of equal_range() is equal to upper_bound() or the second value of equal_range(), then no elements with the same value exist in
the set or multiset. Naturally, in a set the range of
elements that have the same values could contain at most one element.
The following example shows how to use lower_bound(), upper_bound(), and equal_range():
The output of the program is as follows:
If you use a multiset instead of a set, the program has the same output.
Assignments
Sets and multisets provide only the fundamental assignment operations that
all containers provide (table below)
For these operations both containers must have the same type. In particular, the type of the comparison criteria must be the same, although the comparison criteria themselves may be different. See page 191 for an example of different sorting criteria that have the same type. If the criteria are different, they will also get assigned or swapped.
| Operation | Effect |
| c1 = c2 | Assigns all elements of c2 to c1 |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
Iterator Functions
Sets and multisets do not provide direct element access, so you have to use iterators. Sets and multisets provide the usual member functions for iterators (table below)
| Operation | Effect |
| c.begin() | Returns a bidirectional iterator for the first element (elements are considered const) |
| c.end() | Returns a bidirectional iterator for the position after the last element (elements are considered const) |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
As with all associative container classes, the iterators are bidirectional iterators. Thus, you can't use them in algorithms that are provided only for random access iterators (such as algorithms for sorting or random shuffling).
More important is the constraint that, from an iterator's point of view, all
elements are considered constant. This is necessary to ensure that you can't
compromise the order of the elements by changing their values. However, as a
result you can't call any modifying algorithm on the elements of a set or
multiset. For example, you can't call the remove()
algorithm to remove elements because it "removes" by overwriting "removed"
elements the with following arguments (see Section 5.6.2, for a detailed discussion of
this problem). To remove elements in sets and multisets, you can use only member
functions provided by the container.
Inserting and Removing Elements
Table below shows the operations provided for sets and multisets to insert and remove elements.As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.
Table below shows the operations provided for sets and multisets to insert and remove elements.As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.
Inserting and removing happens faster if, when working with multiple
elements, you use a single call for all elements rather than multiple
calls.
| Operation | Effect |
| c. insert(elem) | Inserts a copy of elem and returns the position of the new element and, for sets, whether it succeeded |
| c. insert(pos, elem) | Inserts a copy of elem and returns the position of the new element (pos is used as a hint pointing to where the insert should start the search) |
| c. insert (beg,end) | Inserts a copy of all elements of the range [beg,end) (returns nothing) |
| c. erase(elem) | Removes all elements with value elem and returns the number of removed elements |
| c. erase(pos) | Removes the element at iterator position pos (returns nothing) |
| c. erase(beg,end) | Removes all elements of the range [beg,end) (returns nothing) |
| c. clear() | Removes all elements (makes the container empty) |
Note that the return types of the insert functions differ as follows:
-
Sets provide the following interface:
-
Multisets provide the following interface:
The difference in return types results because multisets allows duplicates,
whereas sets do not. Thus, the insertion of an element might fail for a set if
it already contains an element with the same value. Therefore, the return type
of a set returns two values by using a pair structure,
-
The member second of the pair structure returns whether the insertion was successful.
-
The member first of the pair structure returns the position of the newly inserted element or the position of the still existing element.
In all other cases, the functions return the position of the new element (or
of the existing element if the set contains an element with the same value
already). The following example shows how to use this interface to insert a new element
into a set. It tries to insert the element with value 3.3 into the set c:
If you also want to process the new or old positions, the code gets more
complicated:
The output of two calls of this sequence might be as follows:
Note that the return types of the insert functions with an additional
position parameter don't differ. These functions return a single iterator for
both sets and multisets. However, these functions have the same effect as the
functions without the position parameter. They differ only in their performance.
You can pass an iterator position, but this position is processed as a hint to
optimize performance. In fact, if the element gets inserted right after the
position that is passed as the first argument, the time complexity changes from
logarithmic to amortized constant. The fact that the return type
for the insert functions with the additional position hint doesn't have the same
difference as the insert functions without the position hint ensures that you
have one insert function that has the same interface for all container types. In
fact, this interface is used by general inserters. To remove an element that has a certain value, you
simply call erase():
Unlike with lists, the erase() member function does
not have the name remove(). It behaves differently because
it returns the number of removed elements. When called for sets, it returns only
0 or 1. If a multiset contains duplicates, you can't use erase() to remove only the first element of these
duplicates. Instead, you can code as follows:
You should use the member function find() instead of
the find() algorithm here because it is faster. Note that there is another inconsistency in return types here. That is, the
return types of the erase() functions differ between
sequence and associative containers as follows:
-
Sequence containers provide the following erase() member functions:
-
Associative containers provide the following erase() member functions:
The reason for this difference is performance. It might cost time to find and
return the successor in an associative container because the container is
implemented as a binary tree. However, as a result, to write generic code for
all containers you must ignore the return value.
Exception Handling
Sets and multisets are node-based containers, so any failure to construct a node simply leaves the container as it was. Furthermore, because destructors in general don't throw, removing a node can't fail. However, for multiple-element insert operations, the need to keep elements sorted makes full recovery from throws impractical. Thus, all single-element insert operations support commit-or-rollback behavior. That is, they either succeed or they have no effect. In addition, it is guaranteed that all multiple-element delete operations always succeed. If copying/assigning the comparison criterion may throw, swap() may throw.
Examples of Using Sets and Multisets
The following program demonstrates some abilities of sets:
At first, the type definition
defines a short type name for a set of ints with
descending order. After an empty set is created, several elements are inserted
by using insert ():
Note that the element with value 5 is inserted twice.
However, the second insertion is ignored because sets do not allow
duplicates. After printing all elements, the program tries again to insert the element
4. This time it processes the return values of insert().
The statement
creates a new set of ints with ascending order and
initializes it with the elements of the old set.
Both containers have different sorting criteria, so their types differ and
you can't assign or compare them directly. However, you can use algorithms,
which in general are able to handle different container types as long as the
element types are equal or convertible.
The statement
removes all elements up to the element with value 3.
Note that the element with value 3 is the end of the
range, so that it is not removed. Lastly, all elements with value 5 are removed:
The output of the whole program is as follows:
For multisets, the same program looks a bit differently and produces
different results:
In all cases type set was changed to multiset. In addition, the processing of the return value of
insert() looks different:
Because multisets may contain duplicates, the insertion can fail only if an
exception gets thrown. Thus, the return type is only the iterator position of
the new element.
The output of the program changed as follows:
Example of Specifying the Sorting Criterion at Runtime
Normally you define the sorting criterion as part of the type, either by passing it as a second template argument or by using the default sorting criterion less<>. However, sometimes you must process the sorting criterion at runtime, or you may need different sorting criteria with the same data type. In this case, you need a special type for the sorting criterion — one that lets you pass your sorting details at runtime. The following example program demonstrates how to do this:
In this program, RuntimeCmp<> is a simple
template that provides the general ability to specify, at runtime, the sorting
criterion for any type. Its default constructor sorts in ascending order using
the default value normal. It also is possible to pass
RuntimeCmp<>::reverse to sort in descending
order.
The output of the program is as follows:
Note that coll1 and coll2
have the same type, which is used in fill(), for
example. Note also that the assignment operator assigns the elements and
the sorting criterion (otherwise an assignment would be an easy way to
compromise the sorting criterion).
-----------------------------------------------------------------
See Also:
-----------------------------------------------------------------
See Also:
-----------------------------------------------------------------
- Complete Tutorial of C++ Template's
- Standard Template Library Tutorial
- Inter Process Communication Tutorial
- Advance Programming in C & C++
-----------------------------------------------------------------